[latexpage]Bienvenue à toi, cher joueur, dans le monde de la redstone ! Dans cette rubrique, nous allons découvrir le fonctionnement de cette merveilleuse mécanique, fabriquer nos propres systèmes pour finalement devenir un redstoneur expérimenté. Allons, je suis sûr que vous en avez les capacités !
Dans le précédent article, nous avons vu les propriétés des torches de redstone. Dans ce cinquième épisode, nous allons nous intéresser à un immense volet des circuits : les portes logiques.
Autant vous prévenir : nous allons utiliser un formalisme très précis qui peut être difficile à assimiler en une fois. Parcourez ceci à votre rythme et n’hésitez pas à poser des questions s’il subsiste des incompréhensions. De plus, certaines parties sont purement théorique et sont dans des onglets, vous avez le choix de les lire ou non.
Introduction et vocabulaire
On parle souvent de la redstone comme l’équivalent de l’électronique dans Minecraft. L’électronique a permis, sur les bases de la logique classique et de la physique, de faire naître des applications extraordinaires allant des puces électroniques aux ordinateurs. Certains redstoneurs parmi les plus fous ont reproduits des circuits capables d’effectuer dans Minecraft des fonctions d’ordinateurs ! Mais nous n’allons pas de suite produire des circuits aussi complexes sans connaitre les bases.
L’électronique utilise un formalisme et un langage bien à elle. Avant de présenter les fonctions logiques, ce petit détour vers le vocabulaire s’impose.
Si la logique classique s’occupe d’énoncés, une machine redstone ne peut pas comprendre une phrase avec des mots. Il faut donc changer de langage : ce sera le rôle des signaux logiques à ses entrées.
Tout comme une phrase peut être vraie ou fausse, notre fil de redstone peut avoir plusieurs états :
- le câble est alimenté : c’est l’état « vrai » noté l’état 1
- le câble est éteint : c’est l’état « faux » noté l’état 0
C’est exactement sur cette base que fonctionne le système binaire des ordinateurs. Notez qu’ici, on ne s’occupe pas de l’intensité dans le fil : on se limite à deux états.
En logique, une proposition est un énoncé qui est vrai sous certaines conditions et faux sous d’autres. Par exemple, la proposition « Le nombre entier $n$ est pair. » a pour condition la valeur de $n$ : si $n$ vaut 4, la proposition est vraie alors qu’elle sera fausse si $n$ vaut 3.
Les portes logiques fonctionnent comme une proposition logique : elle comporte des entrées (en orange) qui vont définir la valeur d’une sortie (en violet). En fonction des états (0 ou 1) des entrées, elle donne une réponse logique et programmée en sortie, également sous forme d’un signal d’état 1 ou 0.
Evidemment, une porte logique est plus complexe et les signaux d’entrée et de sortie plus complexes, mais nous allons rester avec des portes de base, qui conviennent à cette définition.
Maintenant que l’étape des définitions est passée, nous allons pouvoir parler un peu plus concret : nous allons construire des portes logiques dans Minecraft et illustrer les lois de la logique par l’expérimentation. Cela ne nous empêchera pas de faire un peu de théorie, mais rien de très méchant rassurez-vous.
Une porte basique : la porte NOT (porte NON)
Commençons par les portes logiques les plus simples qu’il existe : une entrée et une sortie.
Dans l’épisode précédent, nous avions étudié la torche de redstone et la propriété qui va nous intéresser aujourd’hui : sa capacité à pouvoir inverser le courant. L’état de la torche dépend de l’alimentation du bloc support, ce qu’il permet d’influencer sur l’alimentation des câbles à la sortie de la torche.
On avait commencé à suggérer qu’il s’agissait d’une porte NOT, nous n’allons développer le sujet avec le vocabulaire de la logique.
Pour simplifier les écritures des portes, on utilisera la notation de logique $\neg A$ pour dire que l’entrée $A$ est passée par une porte NOT. Si l’entrée $A$ est alimentée, $A = 1 \Rightarrow \neg A = 0$ : la sortie $S$ est éteinte, et inversement.
Pour présenter simplement les propriétés des portes, on utilise des tables de vérité. A gauche, les valeurs possibles pour les entrées (ici, une seule entrée $A$ avec deux états possibles) et à droite les valeurs prises par la sortie. Le code couleur est simple : vert pour un fil alimenté, noir pour un fil éteint.
En logique classique, enchaîner deux négations équivaut à n’avoir rien changé : $ \neg ( \neg A ) = A $
C’est ce qui se produit lorsqu’on enchaîne deux inverseurs à torche à la suite. Dans l’épisode précédent, nous avons vu que l’utilisation principale, mais obsolète de nos jours, était la fabrication des répéteurs pour prolonger le courant. Avec l’introduction des répéteurs en tant qu’objet, ces montages sont devenus inutiles.
Un peu de théorie : combien existe-il de portes à une entrée ?
- comme il y a qu’une entrée $A$, il y a deux états possibles : $A=0$ et $A=1$.
- même raisonnement pour la sortie $S$, deux états possibles : $S=0$ et $S=1$.
Pour chaque valeur d’entrée, deux sorties sont possibles, donc on calcule qu’il y a donc $2^2=2 \times 2 = 4$ portes à une entrée et une sortie :
- La « porte OFF » qui donne toujours une sortie $S=0$ :
$A=0 \Rightarrow S=0$ et $A=1 \Rightarrow S=0$
Elle correspond par exemple à un bloc transparent dans le circuit.
- La « porte Id » qui affiche les mêmes états en entrée et en sortie :
$A=0 \Rightarrow S=0$ et $A=1 \Rightarrow S=1$
Elle correspond à ce que fait un câble de redstone à longueur de circuit.
- La porte NOT que nous venons d’étudier :
$A=0 \Rightarrow S=1$ et $A=1 \Rightarrow S=0$
C’est le travail d’une torche de redstone.
- La « porte ON » qui donne toujours une sortie $S=1$ :
$A=0 \Rightarrow S=1$ et $A=1 \Rightarrow S=1$
Elle correspond aux sources permanentes comme un bloc de redstone.
On dit souvent que la porte NOT est la seule porte à une entrée, vous devinez pourquoi : c’est la seule qui apporte une fonctionnalité réellement utile.
Une porte à deux entrées : la porte OR (porte OU)
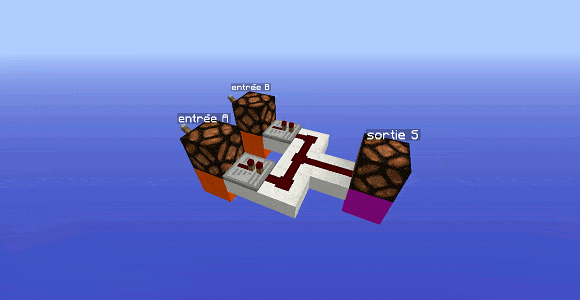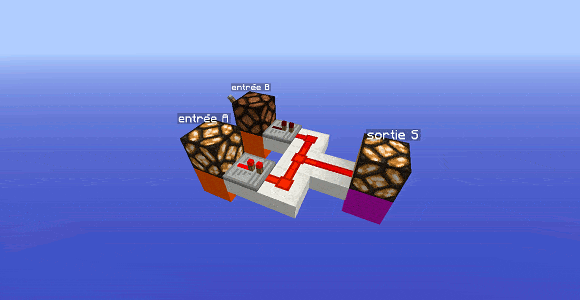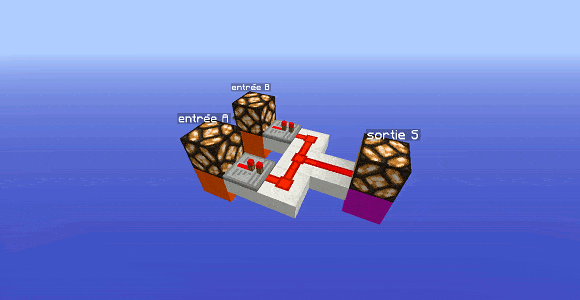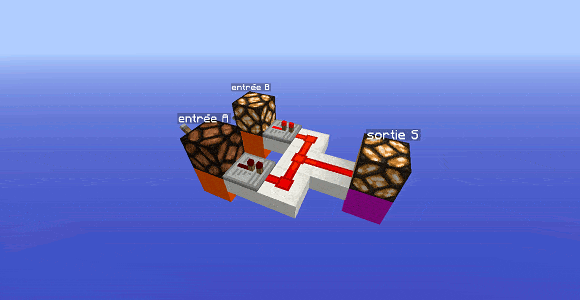
Encore plus simple que la porte précédente : relions les deux entrées ensemble et récupérons en sortie cette réunion de câbles. On a créé une porte OR (porte OU) : la sortie est alimentée si au moins une des entrées est allumée.
Dans l’exemple ci-dessus, les répéteurs ne sont pas nécessaires, ils servent simplement à éviter que le courant remonte alimenter une entrée et allumer une lampe d’une entrée éteinte.
Attention : le « ou » dans le langage courant a des sens très variés. On distingue le « ou inclusif » du « ou exclusif »
- le « ou inclusif » qui est vrai si au moins l’une des conditions est vérifiée. Exemple : si on vous demande si vous parlez anglais ou français, vous pourrez répondre oui si vous parler les deux langues.
- le « ou exclusif » qui, comme son nom l’indique, renvoie faux lorsque les deux choix sont vérifiés. Exemple : si la formule dans un restaurant vous précise « fromage ou dessert », vous ne pourrez avoir les deux.
En logique, le OU par défaut est inclusif. Vous pouvez bien vérifier qu’ici, pour notre porte OR, on a le couple d’entrées $(A=1,B=1)$ qui donne $S=1$ comme le OU inclusif.
La porte OR donne un seul résultat négatif pour trois autres résultats positifs. C’est d’ailleurs un moyen de suspecter qu’il y a une porte OU dans un circuit.
Imaginons qu’on veuille obtenir $S=0$ pour un autre couple d’entrée que $(A=0,B=0)$, par exemple pour le couple $(A=1,B=0)$. Si la valeur pour l’entrée $B$ est correcte, ce n’est pas le cas de l’entrée $A$ qu’il va falloir inverser : c’est donc la porte $\neg A \text{ ou } B$ qui donnera $S=0$ pour le couple voulu.
Jouer avec les négations des entrées permet d’obtenir encore 2 autres portes. Au total, c’est 4 portes à deux entrées qui ont exactement trois sorties $S=1$ et une seule sortie $S=0$.
Une autre porte utile : la porte AND (porte ET)
- Définition de la porte AND
- 1re étape : la porte NOR
- 2de étape : les entrées
- Des versions plus compactes de la porte AND.
- Utilisation des négations aux entrées
Si les portes NOT et OR sont simples à construire, une autre porte parait moins évidente : la porte AND (ou porte ET). Sa signification est simple à comprendre car c’est le même sens que dans le langage courant : seul le couple $(A=1,B=1)$ donne pour résultat en sortie $S=1$. La table de vérité ci-dessus résume la chose.
Il reste ensuite à construire cette porte avec ce que nous savons déjà. Ne vous en faîtes pas, on va vous guider et l’obtenir en deux étapes.
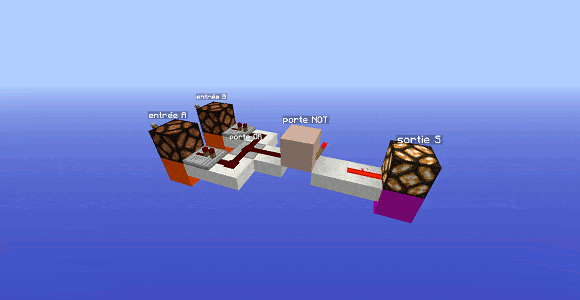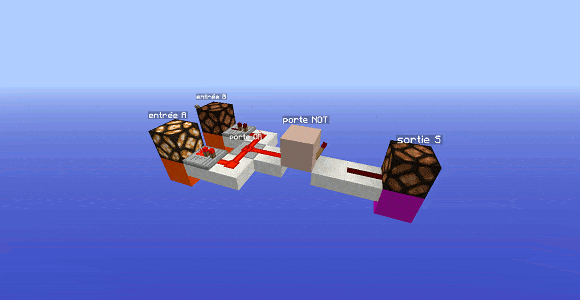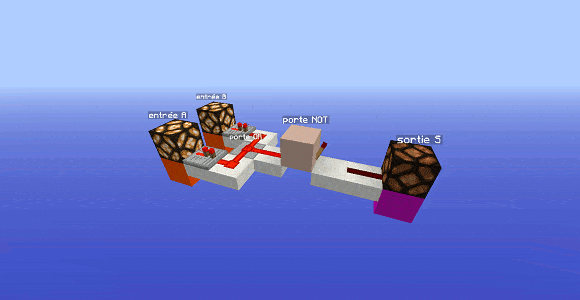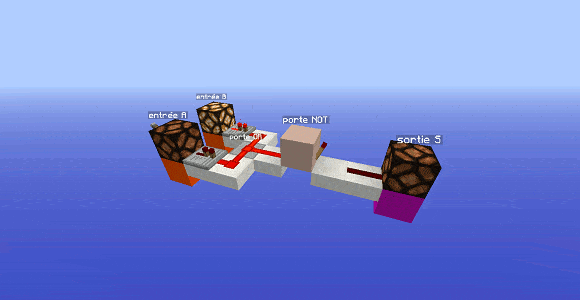
Cette première étape se base sur la constatation suivante : la porte AND est une porte qui possède 1 seule sortie $S=1$ et 3 sorties $S=0$. Or, nous avons des portes qui font exactement l’inverse : les portes dérivées de la porte OR. La porte AND serait donc une inversion de la porte OR.
Inversons donc la sortie d’une porte OR : on obtient ce qu’on appelle la porte NOR (abréviation de NOT OR) : on a déjà une caractéristique de la porte AND d’acquise.
Reste à corriger le couple d’entrées pour lequel on a la sortie $S=1$ : pour la porte NOR, c’est le couple $(A=0,B=0)$, or on désire que ce soit le couple $(A=1,B=1)$.
Il va donc falloir inverser des entrées, même les deux si on se fie aux résultats précédents. On obtient finalement pour la porte AND l’expression suivante :
$S=\neg ( \neg A \text{ ou } \neg B)$
Voici quelques versions plus compactes de la porte AND. A gauche, une version horizontale où vous pouvez distinguer les trois torches des trois inverseurs et la poudre de redstone entre les deux torches qui sert de porte OR.
A droite, il s’agit d’une version verticale ne faisant qu’un bloc de large, idéale pour être cachée dans un mur. Les trois inverseurs sont facilement identifiables mais la porte OR est un peu camouflée : c’est le bloc support du dernier inverseur qui sert de porte : il se fait alimenter par le bas avec une torche et par le haut par la poudre de redstone.
La porte AND, nous l’avons dit, est une porte avec une seule sortie $S=1$. Comme précédemment, en jouant avec les inversions aux entrées de la porte AND, on peut changer le couple concerné.
Au total, c’est 4 portes à deux entrées qui ont exactement trois sorties $S=0$ et une seule sortie $S=1$
Un peu de théorie : les lois de De Morgan
Ce que nous avons utilisé ici illustre ce qu’on appelle, en mathématiques, les lois de De Morgan. Beaucoup d’entre vous les ont vus (ou les verront) en cours lorsqu’on parle ensembles, probabilités et autres.
Elles mettent en évidence les relations entre les opérateurs OU et ET via la négation :
Notre expression de la porte ET peut être déduite de la première loi de De Morgan : il suffit d’en prendre l’inverse et on a bien :
De la seconde loi de De Morgan, on peut déduire la première loi et réciproquement : il suffit d’inverser l’entrée $A$ de chaque côté de l’expression, puis de faire de même avec l’entrée $B$. On utilise la propriété de la double négation pour cela :
Un peu plus technique : la porte XOR (porte OU exclusif)
- Définition de la porte XOR
- Exemple d'une porte XOR
- Etude du modèle éclaté
- Etude d'une moitié
- Retour à la porte complète
- Utilisation des négations aux entrées
Parlons de notre dernière porte : la porte OU exclusif (porte XOR) dont nous avons parlé en passant plus haut.
Ici, on a $S=1$ lorsque les deux entrées ont des états différents, ce qui se produit pour deux couples . La table de vérité correspondante diffère donc de celle du OR d’une ligne seulement, mais cela suffit à rendre le système plus complexe.
Pour écrire cette porte, nous allons utiliser les portes AND que nous avons obtenues en jouant avec les négations. Les deux cas qui donnent une réponse positive dans la porte XOR sont :
- le couple $(A=1,B=0)$, seul couple qui donne une sortie positive à la porte $A \text{ et } \neg B$.
- le couple $(A=0,B=1)$, seul couple qui donne une sortie positive à la porte $\neg A \text{ et } B$.
Si on relie ces deux portes AND par une porte OR, l’expression a bien deux sorties $S=1$ et deux sorties $S=0$, puisque les deux portes AND ne sont jamais vérifiée ne même temps. Une expression de la porte XOR est donc :
$A \text{ xor } B = ( \neg A \text{ et } B ) \text{ ou } ( A \text{ et } \neg B)$
Regardons une porte XOR dans Minecraft : elle est nettement plus compliquée que ne le laisse imaginer l’expression précédente. En effet, cela entraînerait beaucoup de croisements de fils et des problèmes lorsqu’on compacte les deux portes AND différentes.
Reste à savoir comment fonctionne cette porte, c’est-à-dire son expression logique. On va éclater le modèle compacté pour mieux voir.
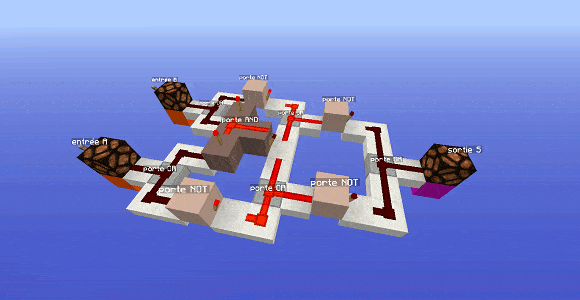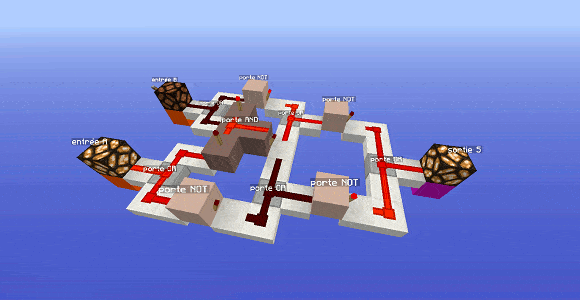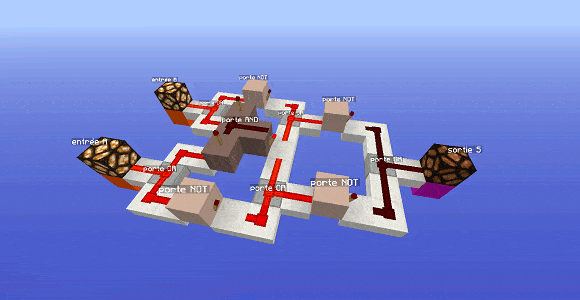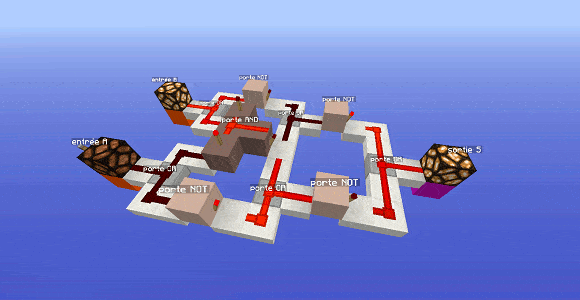
Si on éclate le modèle précédent, on remarque deux choses :
- la présence d’une seule porte AND centrale.
- le circuit est composé de deux parties symétriques qui utilisent la porte AND centrale.
- les deux parties symétriques débouchent sur une seule porte OR finale.
Si on regarde attentivement (ou vous pouvez me croire sur parole, mais c’est plus intéressant si vous essayez), l’expression de cette porte est la suivante :
$S= \neg \, (\neg A \text{ ou } (A \text{ et } B)) \text{ ou } \neg \, (\neg B \text{ ou } (A \text{ et } B))$
Pour simplifier l’étude de notre circuit, on va simplement étudier un morceau de la porte OR centrale. L’expression de départ :
$[preamble]\usepackage{amssymb,amsmath,color}[/preamble]\definecolor{Blue}{RGB}{00,00,255} \definecolor{Red}{RGB}{255,00,00}
S = {\color{Blue} \neg \, (\neg A \text{ ou } (A \text{ et } B))} \text{ ou } {\color{Red} \neg \, (\neg B \text{ ou } (A \text{ et } B))}$
sera écrite sous la forme simplifiée $[preamble]\usepackage{amssymb,amsmath,color}[/preamble] \definecolor{Blue}{RGB}{00,00,255} \definecolor{Red}{RGB}{255,00,00} \text{} S = {\color{Blue} S_1} \text{ ou } {\color{Red} S_2}$ en deux parties :
$[preamble]\usepackage{amssymb,amsmath,color}[/preamble]\definecolor{Blue}{RGB}{00,00,255} {\color{Blue} S_1 = \neg \, (\neg A \text{ ou } (A \text{ et } B))}$
$[preamble]\usepackage{amssymb,amsmath,color}[/preamble]\definecolor{Red}{RGB}{255,00,00} {\color{Red} S_2 = \neg \, (\neg B \text{ ou } (A \text{ et } B))}$
Remarquez qu’on passe d’une expression à l’autre en remplaçant l’entrée $A$ par la porte $B$ et vice-versa.
On va s’intéresser à la moitié $[preamble]\usepackage{amssymb,amsmath,color}[/preamble]\definecolor{Blue}{RGB}{00,00,255} {\color{Blue} S_1 = \neg \, (\neg A \text{ ou } (A \text{ et } B))}$ qui est la partie avant de la porte. Si on trace sa table de vérité, on constate :
- que c’est une porte avec trois sorties $S=0$ et une sortie $S=1$.
- que le seul couple pour lequel $S=1$ est $(A=1,B=0)$.
De ces deux informations, on peut en déduire respectivement que :
- il s’agit d’une porte AND, puisque ce sont les seules à avoir trois sorties $S=0$ et une sortie $S=1$.
- il s’agit de la variante $A \text{ et } \neg B$, puisque c’est celle qui vaut $S=1$ pour le couple $(A=1,B=0)$.
On en déduit alors finalement que $[preamble]\usepackage{amssymb,amsmath,color}[/preamble]\definecolor{Blue}{RGB}{00,00,255} {\color{Blue} S_1 = A \text{ et } \neg B$.
$[preamble]\usepackage{amssymb,amsmath,color}[/preamble]\definecolor{Blue}{RGB}{00,00,255} {\color{Blue} S_1 = \neg \, (\neg A \text{ ou } (A \text{ et } B))}$
$[preamble]\usepackage{amssymb,amsmath,color}[/preamble]\definecolor{Red}{RGB}{255,00,00} {\color{Red} S_2 = \neg \, (\neg B \text{ ou } (A \text{ et } B))}$
Remarquez qu’on passe d’une expression à l’autre en remplaçant l’entrée $A$ par la porte $B$ et vice-versa. On a déduit précédemment l’expression de $[preamble]\usepackage{amssymb,amsmath,color}[/preamble]\definecolor{Blue}{RGB}{00,00,255} {\color{Blue} S_1$ :
$[preamble]\usepackage{amssymb,amsmath,color}[/preamble]\definecolor{Blue}{RGB}{00,00,255} {\color{Blue} S_1 = A \text{ et } \neg B$
Par symétrie, on peut déduire la valeur de $[preamble]\usepackage{amssymb,amsmath,color}[/preamble]\definecolor{Red}{RGB}{255,00,00} {\color{Red} S_2$ :
$[preamble]\usepackage{amssymb,amsmath,color}[/preamble]\definecolor{Red}{RGB}{255,00,00} {\color{Blue} S_1 = \neg A \text{ et } B$
C’est la fin de notre calvaire, on a bien retrouvé l’expression initiale de la porte XOR :
$[preamble]\usepackage{amssymb,amsmath,color}[/preamble]\definecolor{Blue}{RGB}{00,00,255} \definecolor{Red}{RGB}{255,00,00}
A \text{ xor } B= {\color{Blue} (A \text{ et } \neg B)} \text{ ou } {\color{Red} (\neg A \text{ et } B)}$
La porte XOR, nous l’avons dit, est une porte qui possède deux sorties $S=1$. Comme précédemment, en jouant avec les inversions aux entrées de la porte XOR, on peut changer les couples concernés.
Mais, au total, on obtient que 2 portes à deux entrées qui ont exactement deux sorties $S=0$ et deux sortie $S=1$. La raison est simple : la porte possède une grande symétrie.
Un peu de théorie : combien existe-il de portes à 2 entrées et une sortie en binaire ?
- nombres de couples d’entrées : il a deux entrées $A$ et $B$, chacune d’entre elle pouvant prendre 2 valeurs distinctes (0 ou 1, binaire). On se retrouve avec $2 \times 2 =4$ couples d’entrées possibles :
- nombre d’états pour la sortie : la sortie $S$ a deux états possibles : $S=0$ et $S=1$ (binaire)
Pour chacun des couples d’entrée, deux états de sorties sont possibles, donc il y a $2^4 = 2 \times 2 \times 2 \times 2 = 16$ portes à deux entrées et une sortie en binaire. On va ensuite classer ses 16 portes en fonction du nombre de fois que la sortie $S=1$ sort dans la table de vérité :
- cas des portes n’ayant aucune valeur de sortie $S=1$ : il s’agit de la porte pour laquelle tous les couples donnent la même réponse $S=0$. Combien y a-t-il de portes où toutes les sorties valent 0 ? Réponse : une seule, la « porte OFF » :
- cas des portes ayant 4 valeurs de sorties $S=1$ : il s’agit de l’opposé de la porte OFF : la « porte ON ». Encore une fois, il y a qu’une possibilité :
- cas des portes ayant 1 seule valeur de sortie $S=1$ : on cherche donc à attribuer $S=1$ à un couple d’entrées parmi 4. Il n’y a que 4 manières de le faire et cela correspond aux variantes de la porte AND.
- cas des portes ayant 3 valeurs de sortie $S=1$ : il s’agit du raisonnement opposé, cela signifie qu’il n’y a qu’un seul coupe tel que $S=0$. On cherche donc à attribuer $S=0$ à un couple d’entrées parmi 4. Il n’y a que 4 manières de le faire et cela correspond aux variantes de la porte OR.
- cas des portes ayant 2 valeurs de sortie $S=1$ : il reste 16-10=6 portes qui correspondent à cette description. On a vu que les portes XOR faisait partie de cette catégorie et il y en a deux différentes :
On peut démontrer que $A \text{ xor } B = \neg A \text{ xor } \neg B$ et $\neg A \text{ xor } B = A \text{ xor } \neg B$, d’où seulement 2 portes.
Reste à trouver les 4 dernières : ce sont les portes qui ne dépendent que d’une seule entrée en oubliant totalement l’autre. En utilisant la fonction NOT, on trouve nos portes manquantes :
On a donc trouvé toutes nos portes possédant deux entrées et une sortie en binaire.
Conclusion
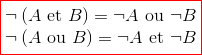
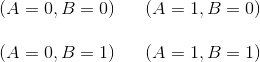
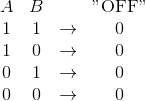
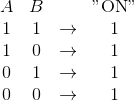
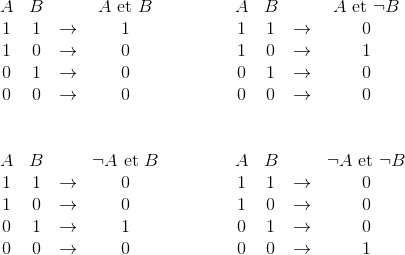
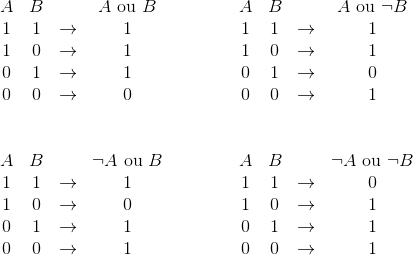
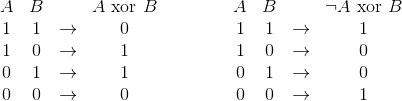
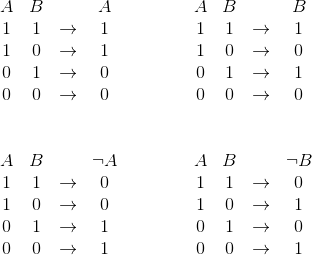
@em1000diams Merci. Par la suite, je compte revenir sur les portes pour présenter réellement différents modèles, ce qui n’est pas possible actuellement parce que nous n’avons vu que la torche de redstone. Dès que les comparateurs, les pistons et autres joyeux items seront présentés… on va commencer à s’amuser. ^^
Très bon article, mais tu ne présente pas énormément de portes, tu devrais parler de gestion de la durée/nombre d’impulsion, des différentes mémoires, du compactage des portes sur le plan horizontal et vertical etc.
@quartz C’est vrai que l’article n’utilise pas beaucoup d’exemples. On pourra citer par exemple les portes ET et OU pour modifier les délais, les XOR pour les lumières, etc.
Le passage par les notations est lourd (très lourd, je le reconnais), mais j’espère pouvoir faire beaucoup plus simple bientôt, dès qu’on aura vu les comparateurs et les répéteurs, ce qui permet de voir d’autres designs. On repassera sur quelque chose de beaucoup plus simple en septembre, rassure-toi. ^^
Peut-être que d’utiliser les notations utilisées en logique risque de perdre pas mal de monde, en attendant, article très bien présenté. Cependant, tu ne donnes pas d’exemples concrets de l’utilisation d’une porte logique (exemple : XOR va-et-viens de lumière dans une pièce) ce qui peut faire penser que leur utilisation se limite aux ordinateurs ou au puces. J’ai moi même longtemps pensé que l’utilisation des portes logiques se limitait aux calculatrices ou aux systèmes énormes qui ont été en vogue un moment sur Minecraft, avant de comprendre leur réelle utilité et surtout qu’on s’en servait sur presque tout les systèmes.
Petit erreur ! A « combien y a t-il de porte logiques » tu as mis deux fois la possibilité (A=1,B=0) au lieu de (A=1,B=0) et (A=0,B=1) … =)
Sinon très bon article, si j’avais eu ça à mes début, j’aurais bien moins galéré ! Moi j’ai appris avec Arno00 puis Aypierre;
Super tuto très complet! Si je n’étais plus en vacances j’aurais vraiment fait attention aux parties techniques de la chose mais c’est génial quand même!
Là on arrive vraiment à du lourd. Je suis content car les autres articles étaient un peu… faciles !
Ça doit être beaucoup de travail pour faire ces articles !
@TheMrZZ C’est vrai qu’il existe de versions beaucoup plus compactes de cette porte (et de beaucoup d’autres d’ailleurs) mais ces modèles utilisent des mécaniques que je n’ai pas encore présente, ici le mode soustraction du comparateur.
Des que nous aurons vu la plupart des éléments (répéteur, comparateur, piston, entonnoir et dropper…), je ne suis pas contre reparler des portes logiques pour présenter d’autres modèles les employant.
Bon article, mais un exemple de porte XOR compacté je serait pas de trop.
Le plus simple étant celui avec 2 leviers, 6 redstones et 2 comparateurs selon moi.