[Tutoriel] Guide Mapmaking: Bonus #2 – Raycasting, orientation, position et … trigonométrie !

Cet article fait partie d’une série servant à enseigner l’art du développement sur Minecraft. Vous pourrez retrouver l’introduction et le sommaire en cliquant ici.

NE FUYEZ PAS ! Oui, il va y avoir des mathématiques mais pas d’inquiétude, on a déjà tout fait pour vous, vous n’aurez pas besoin de faire le moindre calcul !

Nous allons voir en détail ici le fonctionnement d’un système de raycasting qui fonctionnait même avant l’arrivée de la 1.13 (et des sélecteurs ‘^’) et qui conserve encore aujourd’hui une foule d’avantages (que ce soit niveau optimisation ou fonctionnalités). Pour cela, nous allons donc aborder un sujet très important dans tous les jeux : la position et l’orientation des objets. Dans certains jeux, où cette partie se doit d’être précise et complète (ceux qui se déroulent dans l’espace notamment), il faut définir la position de l’objet ainsi que l’orientation de sa tête, mais le corps entier peut aussi être orienté selon un certain axe, et il peut même encore pivoter sur cet axe. Ce qui commence à faire pas mal de variables à considérer. Dans Minecraft, fort heureusement, cette partie est grandement simplifiée car le jeu se déroule toujours à proximité du sol et le joueur a toujours les pieds en bas. Il a donc uniquement sa position (3 valeurs en X, Y et Z pour le positionner dans l’espace) et l’orientation de sa tête (que nous appellerons Phi et Theta, vous l’avez peu être déjà vu dans certains jeux sous le nom de Yaw et Pitch). L’orientation de son corps suit en permanence celle de sa tête donc nous n’aurons pas à nous en soucier.

Système de coordonnées

Certains d’entre vous se demandent peut-être comment on représente cette orientation, à quoi correspondent ces Phi et Theta. Il s’agit en fait d’un système de coordonnées particuliers appelée “coordonnées sphériques”. Concrètement, le système de coordonnées classique (appelé “cartésien”) consiste à placer 3 axes tous perpendiculaires entre eux (les 3 axes visibles lorsque vous appuyez sur ‘F3’. La position est donc définie par la longueur entre le centre de ces 3 axes et le point le plus proche de l’objet sur chacun d’eux. En coordonnées sphériques, les 3 composantes ne suivent pas la même logique. Au lieu d’avoir les variables X, Y et Z, toutes les 3 correspondant à des distances, nous aurons donc Phi, Theta et R. Phi et Theta sont 2 angles, l’un est l’angle horizontal entre la demi-droite Phi=0 et Theta=0 et la droite qui coupe la position de l’objet et la position du centre du repère et est donc définie de 0 à 360°. Theta suit la même logique, mais représente cette fois-ci l’angle formé sur un plan vertical. Enfin, R représente la distance entre l’origine du repère et la position de l’objet.

Voici un petit schéma illustrant les deux systèmes de coordonnées :

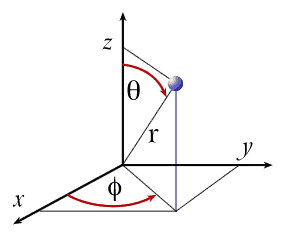
Si vous vous dites “mais pourquoi utiliser ce système de coordonnées ? Il est plus complexe et pour au final faire la même chose non ?” et bien, détrompez vous. Ce système permet d’effectuer des calculs de façon très simple et est très souvent utilisé par les mathématiciens, physiciens et ingénieurs. Dans le cas de l’orientation, on en voit tout de suite l’intérêt : 2 valeurs suffisent à décrire la droite formée par la visée du joueur. Si il bouge horizontalement, il suffit de baisser ou augmenter Phi et si il bouge verticalement, il suffit d’augmenter ou diminuer Theta. En coordonnées cartésienne, il faudrait repérer un point sur cette droite, lui donner des coordonnées qu’il faudrait recalculer à chaque changement d’orientation. Bref, ce serait galère.

Retour au raycasting

Mais revenons en à nos moutons, ou plutôt à notre raycasting. Ce qu’on va chercher à faire ici, c’est de faire en sorte qu’une entité puisse envoyer un projectile devant lui à une certaine vitesse. Avec la 1.13, on peut simplement créer le projectile, le téléporter sur l’entité qui tire (qu’on va appeler Bob) afin que le projectile prenne la même orientation que Bob. Ensuite, il suffit de téléporter le projectile en “^ ^ ^1” pour qu’il avance d’un bloc devant lui à chaque fois.

C’est un bon début, mais d’une part on ne gère pas la vitesse, on la définit à l’avance (^ ^ ^1 -> la vitesse sera de 1 bloc/tick, soit 20 blocs/seconde) sans pouvoir la modifier et d’autre part, si on veut modifier la trajectoire pour par exemple simuler la gravité, cette modification ne se fera pas comme on le souhaite (la gravité accélère de façon continue alors que votre résultat donnera une accélération qui deviendra de plus en plus petit jusqu’à s’arrêter totalement lorsque le projectile visera vers le bas).

Rappel sur la dichotomie

Pour résoudre ces problèmes, il va falloir décomposer en plusieurs petits problèmes, car tenter de le résoudre comme ça est pratiquement impossible sans se casser les dents dessus pendant plusieurs années. Le premier problème (la gestion de la vitesse) semble assez évident : il faudrait pouvoir mettre une variable dans la téléportation ! Sauf que… on peut pas… dommage. À moins que, vous connaissiez la dichotomie ? Si vous répondez non, vous êtes un mauvais élève, retournez voir le premier article bonus qui porte dessus !

C’est bien beau, mais comment on va appliquer cette dichotomie dans Minecraft ?

Et bien, la variable sera notre vitesse (qui est notre nombre inconnu) et nous allons appliquer un certain nombre de tests pour la retrouver. Avant tout, il va falloir savoir dans quel intervalle se trouve notre nombre, intervalle qui va définir notre vitesse maximum … ou pas, on verra plus tard comment l’outre passer. Imaginons que notre intervalle va de 0 à 1000 (1000 équivalent à une vitesse de 1 bloc par tick). Vous vous attendez à ce que je vous dise de tester 500 ? On pourrait, mais ce ne serait pas très propre car vous arriverez à un moment où, à force de diviser par 2, vous arriverez sur un nombre décimal, et vous ne saurez pas si il faut choisir le nombre entier supérieur ou inférieur. Pour éviter ça, il va falloir travailler avec des puissances de 2 (2^n, soit -> 0,1,2,4,8,16,32,64,128,256 et 512). De cette façon, nous sommes sur que toutes les divisions par 2 donneront toujours un nombre entier !

Application de la dichotomie dans notre problème

Nous allons donc commencer par tester 512 (la puissance de 2 directement supérieur à 500):

/execute as @e[tag=Projectile,scores={Vitesse=512..}] at @s run tp @s ^ ^ ^0.512
/scoreboard players remove @e[tag=Projectile,scores={Vitesse=512..}] Vitesse 512

Hein ? C’est quoi tout ça ?

Regardez bien, c’est assez subtile : je téléporte tous les projectiles ayant un score “vitesse” au dessus de 512 à 0,512 bloc devant eux, puis je leur retire 512. Vu que le score vitesse ne peut être compris que entre 0 et 1000 (car pour le moment, on se contente d’une vitesse comprise entre 0 et 1 bloc/tick, soit 20 blocs/seconde), alors plus aucun projectile ne se trouve avec un score Vitesse supérieur à 512 ! Si je répète l’opération en divisant par 2:

/execute as @e[tag=Projectile,scores={Vitesse=256..}] at @s run tp @s ^ ^ ^0.256
/scoreboard players remove @e[tag=Projectile,scores={Vitesse=256..}] Vitesse 256

Alors plus aucun projectile n’a de score Vitesse supérieur à 256, et tout ceux qui se trouvaient au dessus on été déplacés de 0,256 blocs. Mais c’est pas tout ! Les projectiles qui avaient un score au dessus de 768 (512 + 256) ont été déplacés 2 fois ! Une fois de 0,512 et l’autre fois de 0,256 blocs, et se trouvent maintenant avec un score en dessous de 256 !

Et si on cumule ça jusqu’à arriver à 1 (en divisant par 2 les valeurs à chaque fois), on se rend compte que, pour n’importe quelle valeur entre 0 et 1000, notre projectile s’est déplacé d’autant de milli-bloc vers l’avant ! Le tout en 10 étapes de deux commandes chacune, soit 20 commandes pour gérer une vitesse possédant 1000 variations différentes ! Et ce qu’il y a d’encore plus fou, c’est que si on veut aller à une vitesse de 2 blocs par tick (et donc avoir un score Vitesse entre 0 et 2000), il n’y aura qu’une seule étape à ajouter au début, celle pour 1024, ce qui fera un total de 22 commandes ! On a multiplié par 2 les possibilités en ajoutant seulement 2 commandes !

Et la gravité alors ?

Bon, c’est bien, maintenant on a un projectile qui peut avoir une vitesse presque infinie (il est rarement utile de dépasser les 10 bloc par tick, le jeu ne le supporte pas vraiment). Mais maintenant, il faut résoudre le problème de la gravité (ou du vent, ou autre modification de trajectoire qui se fait mal si on touche à l’orientation du projectile). Pour cette partie, nous allons devoir comprendre comment fonctionnent les coordonnées locales (^L ^U ^F). Mais avant ça, posons nous la question : comment appliquer la gravité ? Logiquement, il faut accélérer notre projectile sur l’axe verticale (axe Y) et cela de façon constante. Or, avec les coordonnées locales, on n’a pas d’axe Y, donc on ne va pas pouvoir appliquer la gravité directement dessus. Mais à vrai dire, comment le jeu sait à quel endroit vous téléporter lorsque vous exécutez la commande “/tp @s ^ ^ ^1” ? Je veux dire, le jeu doit bien avoir un moyen de déterminer la position X Y et Z où vous allez arriver, donc il doit y avoir un lien entre ^L ^P ^F (Left, Up et Front) et X, Y et Z ! Et bien oui, et ce lien, c’est le changement de système de coordonnées !

En réalité, les coordonnées locales sont des coordonnées de type cartésiennes (3 axes infinis et perpendiculaires entre eux) dont l’orientation et la position sont synchronisées avec l’orientation et la position de l’entité (alors que l’origine des coordonnées X Y et Z sont toujours placé au même endroit sur la map et les axes ne tournent jamais). On se rend donc compte que les coordonnées locales dépendent directement des coordonnées sphériques qu’on a vu précédemment (utilisant Theta et Phi pour l’orientation). Je vous le donne en mille, ce qui relie Theta, Phi, R et X, Y et Z, c’est les relations:

• X = R * cos(Phi) * sin(Theta)
• Y = R * cos(Theta)
• Z = R * sin(Phi) * sin(Theta)

Oulà ! Je croyais qu’il n’y avait pas de calcul à faire !

Pas d’inquiétude, si vous êtes en 1.13, vous n’allez même pas avoir besoin d’utiliser ça. Sinon, vous devrez soit coder des fonctions (ou en command-blocks si vous êtes entre la 1.9 et la 1.11, avant la 1.9, c’est malheureusement impossible :/) pour calculer les sinus et cosinus, soit télécharger notre magnifique librairie (ou notre LGdir si vous êtes avant la 1.12) qui le fera pour vous (et on ne paye même pas pour ce placement de produit !)

Changeons de système de coordonnées

Bref, vous l’aurez compris, pour appliquer notre gravité, on va plutôt travailler avec X, Y et Z. C’est là qu’il va falloir ruser, car pour savoir comment faire varier X, Y et Z en fonction de l’orientation, il existe deux solutions selon votre version du jeu :

• 1.12 et avant : On utilise les relations mathématiques ci-dessus en récupérant l’orientation du projectile (Phi et Theta) puis en calculant X, Y et Z (en considérant que R=1, cf. le schéma du début pour voir à quoi correspond R)
• 1.13 et après : On utilise une fois la téléportation à un bloc vers l’avant avec les coordonnées locales (^ ^ ^1) et on calcule la différence de position entre avant et après (en enregistrant les deux puis en les soustrayant). De là, on aura… un vecteur !

Si on répète l’opération qu’on a vu tout à l’heure avec la dichotomie, on sait comment bouger notre projectile sur chacun des axes (on a maintenant 3 variables: VitesseX, VitesseY et VitesseZ qu’on traitera indépendamment).

Mais du coup, pour appliquer la gravité, il ne reste plus qu’à retirer en permanence de la vitesse sur Y non ?

Eh bien … OUI ! Mais combien ? On va le voir tout de suite ! On sait que la gravité accélère les objets à ~10 mètres par secondes^2 (toutes les secondes, l’objet va gagner une vitesse de 10m/s vers le bas). Hors, ici, on travaille en tick, et un tick c’est 0,05 secondes (1/20ème de seconde). On divise donc 10 par 20^2 (car nous avons des secondes^2) ce qui donne 0,025 m/tick et on sait que 1 bloc = 1 mètre. Du coup, il faut retirer à chaque tick 0,025 sur le vecteur Y de notre projectile. Sauf que, nous ne pouvons pas avoir de nombre à virgule dans notre score, ce pourquoi on a dit que 1000 = 1 bloc, il faut donc multiplier 0,025 par 1000 soit 25 ! Il faut donc, à chaque tick, retirer 25 au score VitesseY du projectile ! C’est tout !

Conclusion

Pour faire un projectile que vous pouvez ensuite manipuler comme bon vous semble, vous devrez:

• Récupérer l’orientation de Bob (l’entité qui tire)
  • 1.9 -> 1.12: via la dichotomie et les arguments de sélection “ry,rym,rx et rxm”
  • 1.13 et +: récupération via /execute store
• Créer un vecteur à partir de cette orientation
  • 1.9 -> 1.12: calcul de trigonométrie (oups, le mot interdit !)
  • 1.13 et +: création d’entité 1 bloc devant puis calcul de la différence de position
• Mettre le projectile en mouvement
  • Via la dichotomie

Si vous ne comprenez pas, alors vous devriez relire plus doucement ;)

Cet exemple nous tenait à cœur car c’est l’exemple parfait pour montrer l’importance de décomposer son problème en tout petits problèmes. Cette simple pratique peut permettre de résoudre des problèmes qui semblent être impossible et permet ainsi d’ouvrir des portes sur des systèmes encore plus complexes !