[Tutoriel] Guide MapMaking : Bonus #1 – Dichotomie et arbre de recherche

Cet article fait partie d’une série servant à enseigner l’art du développement sur Minecraft. Vous pourrez retrouver l’introduction et le sommaire en cliquant ici.

Bon, le développement c’est bien, mais ça devient vraiment intéressant lorsqu’on arrive à trouver des solutions simple à des problèmes qui paraissent énormes ! Jouons donc à un petit jeu pour illustrer la solution à un problème qui arrive souvent dans le développement, sous des formes diverses et variées.

Dichotomie – Exemple

Nous allons tirer un nombre entre 0 et 1000 et vous devrez trouver ce nombre en 10 coups. A chaque coup raté, vous savez si le nombre que vous cherchez est plus grand ou plus petit que le nombre que vous avez choisis. Certains ont reconnu là le principe du Juste Prix.

Intuitivement, on peut penser qu’on a que 1 chance sur 100 de trouver le bon nombre avec 10 coups. D’un autre côté, on est toujours tenté de taper au milieu (donc proche de 500) au premier coup parce que… une petite voix dit que c’est la meilleure option. En réalité, il y a une méthode pour trouver le nombre a coup sur grâce à la technique que votre intuition essaye de vous montrer : la dichotomie.

Le principe est simple: diviser le champ de recherche en deux et éliminer celui qui est mauvais.

Ici, en choisissant 500, l’information “c’est plus !” ou “c’est moins !” vous donnera l’information sur quel partie éliminer. Vous aurez donc un champ de recherche qui sera désormais constitué de 500 nombres au lieu de 1000 et tout ça en … 1 étape.

Répétons donc cette opération a chaque fois, et on se rend compte que la taille du champ est divisé par 2 a chaque coups soit :

• 1er coup: 1000 -> 500
• 2ème coup: 500 -> 250
• 3ème coup: 250 -> 125
• 4ème coup: 125 -> 63
• 5ème coup: 63 -> 32
• 6ème coup: 32 -> 16
• 7ème coup: 16 -> 8
• 8ème coup: 8 -> 4
• 9ème coup: 4 -> 2
• 10ème coup: Vous devrez choisir entre les deux nombres restant, pas le choix, il faut y aller au hasard.

Ouais, pas si “à coup sûr” que ça finalement !

C’est vrai, même avec cette technique, il restera toujours une part de hasard, il faudrait un 11ème coup pour éliminer ce hasard totalement.

En revanche, vous pourrez remarquer qu’au 4ème et 5ème coup, le nombre des possibilités n’a pas vraiment été divisé par deux. En effet cette petite simulation est très pessimiste car, pour arriver à un champ de 2 possibilités au dixième coup, elle admet que vous avez fait 2 mauvais choix au préalable. Or, vous n’aviez qu’une chance sur deux de faire chacun des mauvais choix (sans savoir lequel était bon et lequel était mauvais), et donc vous avez 1 chance sur 4 de faire les deux mauvais choix. Enfin, si vous perdez, cela voudra dire que vous avez fait une troisième mauvais choix. Il y a donc au final une probabilité de 1/2³ soit 1 chance sur 8 de perdre ! C’est toujours beaucoup mieux que 1 chance sur 100 de gagner comme on avait au début !

Dichotomie – Théorie

Donc nous avons vu que pour trouver un nombre entre 0 et 1000, il faut 10 coups dans le pire des cas (oui car si le nombre est 250 par exemple, il n’en faudra que 2), mais comment généraliser ce nombre de coup à n’importe quel intervalle ? Combien faudra-t-il de coup pour trouver une valeur entre 0 et 4096 par dichotomie ?

Attention on va parler de mathématiques car il existe bien une formule assez simple : 

log₂(N) où N est le nombre d’élément. 

Pour ceux qui ne connaissent pas la fonction log₂ (à lire logarithme en base 2), elle fait exactement l’opposé (réciproque) de la base de 2, je m’explique :

2³ = 8 donc log₂(8) = 3

Le log₂ renvoie donc l’exposant auquel doit être élevé 2 pour obtenir 8 (ici 3).

Pour généraliser un peu :

2ⁿ = m donc log₂(m) = n

Reprenons notre exemple avec l’intervalle [0;1000], ici nous avons donc 1001 valeurs (de 1 à 1000 + la valeur 0), appliquons notre formule :

log₂(1001) ≈ 9.97

Sachant que l’on ne travaille qu’avec des nombres entiers (ce serait stupide de trouver une valeur en 9.97 coups, non ?), on arrondit au supérieur, ce qui donne bien, ici, 10 ! Il faudra alors bel et bien 10 coups pour trouver un nombre caché dans lintervalle [0;1000] !

Dichotomie – Pratique

Bon, c’est bien beau de trouver un nombre mais en réalité les problèmes sont rarement aussi simples… ou pas. Là où la dichotomie est compliquée, ce n’est pas dans le fait de l’appliquer, car on a vu que le principe est très simple. Le plus dur sera de savoir quand et comment l’utiliser. Par exemple dans Minecraft, quand vous souhaitez détecter quel est le bloc présent sous vos pieds.

En regardant les commandes disponibles, on se rend compte qu’on n’a pas trop le choix, il faut tester chaque type de bloc un à un et voir lequel s’avère être le bon. Difficile à mettre en pratique au vu du nombre de blocs existant et du nombre de variantes de ces derniers. Pourtant, c’est l’un des cas les plus compliqués où la dichotomie va jouer un rôle crucial. Voici le raisonnement utilisé pour mettre en place un detection du bloc par la dichotomie:

Peut-on regrouper les éléments ?
– Leur nom n’étant pas des chiffres, difficile de regrouper les blocs “de 0 à 500”. On peut donc encore moins savoir si le résultat sera supérieur ou inférieur.
– Par contre, on peut quand même former des groupes de bloc avec les tags de bloc (si vous ne savez pas de quoi je parle, ce n’est pas dites vous que c’est un peu comem les tags d’entité que nous avons vu précédement, mais pour les blocs. Pour ceux qui veulent en savoir plus, je vous redirige vers le wiki) et on peut tester si le bloc qu’on cherche appartient à ce groupe, donc OUI, on peut les regrouper !

Peut-on éliminer des groupes ?
– Et bien, oui, il suffit de tester si le bloc appartient à un groupe particulier. A partir de là, si on sépare tous les blocs en deux partie et qu’on test un groupe, il n’y aura que deux solutions possibles: soit le bloc appartient au groupe qu’on test et on peut éliminer l’autre groupe, soit il n’appartient pas au groupe qu’on cherche et on peut éliminer le groupe cherché.

Peut-on hierarchiser ces groupes ?
Cette question est cruciale car sans hierarchisation des groupes, imposible de savoir où vous en être dans l’algorithme, quels groupes vous avez déjà testé et quels groupes ils vous rester à tester. On a dit qu’on le peut pas compter sur des intervalles de nombre (intervalles qui servent de groupe) car ici, on manipule des noms de bloc. Cependant, cette question est le coeur d’un des soucis les plus fréquents : elle n’est pas adaptée à tous les cas de figure pouvant faire intervenir la dichotomie. En tout cas, posée comme ça, elle n’est pas évidente. C’est pourquoi nous allons nous poser une autre question, qui à pour propriété de répondre à celle-ci:

Un élément (ici un bloc) peut-il appartenir à plusieurs groupes ?
– Et oui, une fois qu’on a éliminé un groupe, vous vous doutez surement qu’il faut répéter l’opération jusqu’à ce que le groupe ne soit formé que d’un seul bloc. Chaque groupe devra donc être divisé en 2 groupes pour le test suivant, et chacun de ces deux groupes devront être eux même divisés en deux groupes etc … Bref, il faut absolument qu’un élément puisse appartenir à plusieurs groupes. Ici c’est le cas ! Un bloc peut appartenir à plusieurs tags.

Bon ben c’est bien parti, il ne reste plus qu’à créer tous ces groupes et à les tester un par un mais… Est-ce qu’on gagne vraiment en efficacité à tester tous les groupes ? Oui car justement, on ne les testera pas tous, les groupes appartenant à un groupe déjà éliminé ne seront pas testés ! Comment faire ça ? En construisant ce qu’on appelle un arbre binaire ! Lorsqu’un groupe est éliminé, il suffira de lancer la fonction qui testera les sous-groupes présents dans le groupe qui n’a pas été éliminé. Et parce qu’un schéma vaut mieux qu’une longue explication, voilà un schéma qui montre comment l’algorithme à testé les groupes:

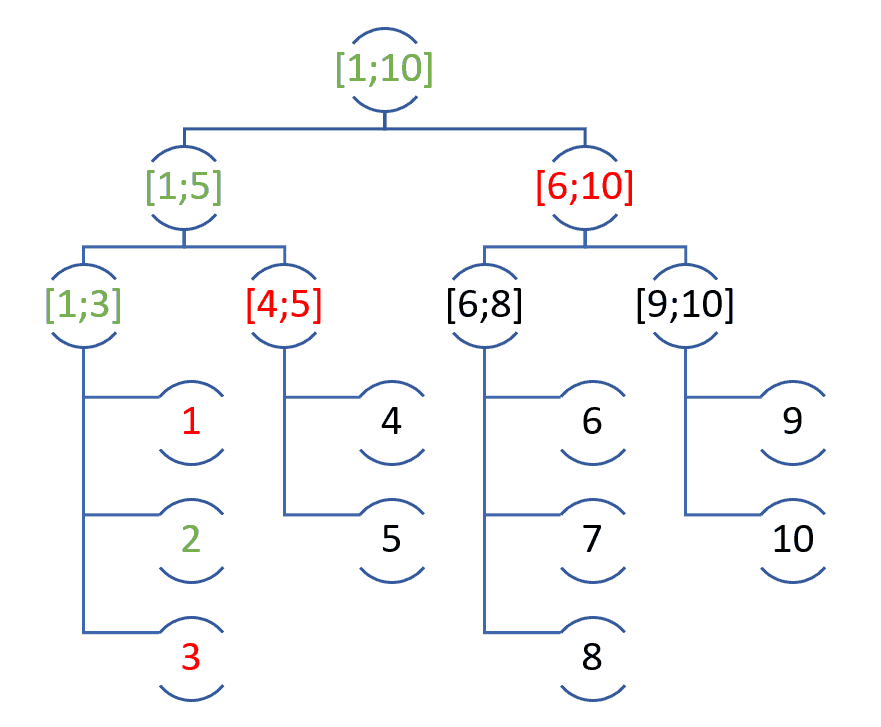
En vert, les groupes testés qui ont été retenus car l’élément qu’on cherche appartient à ce groupe. En rouge, les groupes testés qui n’ont pas été retenu car l’élément cherché n’appartient pas au groupe.

On voit que, même avec 10 éléments, l’algorithme est rentable car il ne fait que 8 tests (tous ceux colorés en vert ou rouge) au lieu de tester les 10 éléments. 8 au lieu de 10, c’est pas incroyable comme optimisation, mais plus le nombre d’élément augmente, plus ça devient rentable car rappelez vous, le nombre de test évolue en fonction du logarithme en base 2 du nombre total d’élément à tester !

Dans notre cas c’est pareil, sauf qu’au lieu d’avoir des intervalles de nombre, on aura des tags de blocs. Cependant, notre cas sera bien plus complexe que ça car fera intervenir plus de 670 blocs (à l’heure actuelle en 1.14.4). développemer un tel algorithme de recherche ne sera donc pas chose facile, à moins de toucher un peu sa bille en programmation dans un autre langage, permettant de générer un tel algorithme en commande et en tags Minecraft.

Roh, mais comment je fais du coup pour faire un tel système ?

Pas de panique, durant ce guide, je ne vous demanderai jamais de faire un système aussi complexe, car ça demande des compétences au delà de Minecraft (en mathématique et en développement). En revenche, nous avons réalisé ce type de système pour vous dans notre Gunivers-Lib. Si vous êtes curieux de voir comment le système fonctionne ou que vous souhaitez l’utilisez, vous pouvez dès maintenant télécherger le datapack et aller jeter un oeil dans le dossier Gunivers-Lib\data\gunivers-lib\functions\object\convert\block. De là, vous trouverez une fonction « block_to_id », qui placera dans votre score « BlockId » l’Id du bloc que vous testez, ou encore « id_to_block », qui à l’inverse, placera un bloc en fonction du score que vous possédez !

Arbre de recherche

Oulà, on arrive à la fin de l’article et on a toujours pas parlé des arbres de recherche ?!

Pas de panique, en réalité, on en a parlé tout au long de cet article, sans même s’en rendre compte ! A chaque fois que nous parlions de hierarchisation, de groupes etc. nous parlions en réalité de branches au sein d’un arbre de recherche.

D’accord mais c’est quoi un arbre de recherche ?

Et bien, vous voyez le graphique que nous avons vu plus haut ? C’est exactement ça ! Chaque élément est placé dans une catégorie, elle même placée dans une catégorie plus grande etc. jusqu’à n’avoir qu’une seule catégorie. Si vous regardez le graphique à l’envers, ça représente (très schématiquement), un arbre !

Ces arbres de recherchent permettent en algorithmie de trouver très efficacement un élément précis parmi un grand nombre d’autres éléments. Il suffit de tester les catégories, de la plus large à la plus petite, en utilisant un algorithme de dichotomie. Vous utilisez d’ailleurs ce système tous les jours sans vous en rendre compte:

• Votre adresse postale: 5 Avenue Anatole, Paris, France est un chemin dans un arbre de recherche permettant de trouver un lieu précis sur Terre parmi un nombre immense de possibilités ! France est donc le premier grande groupe qui réduit la zone de recherche, Paris est le deuxième groupe, plus petit, Anatole se réfère à toutes les voies de circulation portant ce nom, Avenue vient réduire à 1 seul ces dernières et 7 vient donner la position du lieu dans cette Avenue.
• Votre adresse IP : ici, c’est un peu plus compliqué car on parle de 0 et de 1, mais les chiffres les plus à gauche sont les grands groupe auquels vous appartenez (exemple: 192.168… signifie que vous êtres sur un réseau privé de particulier) et les chiffres les plus à drotie servent à vous identifier spécifiquement.
• Et encore beaucoup d’autres…